什么是 hash? 2021-09-04 网络 暂无评论 2903 次阅读 #回答一 转自:https://www.zhihu.com/question/26762707/answer/40119521 首先回答题主的问题。hash(散列、杂凑)函数,是将任意长度的数据映射到有限长度的域上。直观解释起来,就是对一串数据m进行杂糅,输出另一段固定长度的数据h,作为这段数据的特征(指纹)。也就是说,无论数据块m有多大,其输出值h为固定长度。到底是什么原理?将m分成固定长度(如128位),依次进行hash运算,然后用不同的方法迭代即可(如前一块的hash值与后一块的hash值进行异或)。如果不够128位怎么办?用0补全或者用1补全随意,算法中约定好就可以了。原问题回答完毕。但是既然要说hash算法,不妨说的更透彻些。 --- 由于用途的不同,hash在数据结构中的含义和密码学中的含义并不相同,所以在这两种不同的领域里,算法的设计侧重点也不同。预备小知识:抗碰撞能力:对于任意两个不同的数据块,其hash值相同的可能性极小;对于一个给定的数据块,找到和它hash值相同的数据块极为困难。抗篡改能力:对于一个数据块,哪怕只改动其一个比特位,其hash值的改动也会非常大。在用到hash进行管理的数据结构中,比如hashmap,hash值(key)存在的目的是加速键值对的查找,key的作用是为了将元素适当地放在各个桶里,对于抗碰撞的要求没有那么高。换句话说,hash出来的key,只要保证value大致均匀的放在不同的桶里就可以了。但整个算法的set性能,直接与hash值产生的速度有关,所以这时候的hash值的产生速度就尤为重要,以JDK中的String.hashCode()方法为例: ``` public int hashCode() { int h = hash; //hash default value : 0 if (h == 0 && value.length > 0) { //value : char storage char val[] = value; for (int i = 0; i < value.length; i++) { h = 31 * h + val[i]; } hash = h; } return h; } ``` 很简洁的一个乘加迭代运算,在不少的hash算法中,使用的是异或+加法进行迭代,速度和前者差不多。 在密码学中,hash算法的作用主要是用于消息摘要和签名,换句话说,它主要用于对整个消息的完整性进行校验。举个例子,我们登陆知乎的时候都需要输入密码,那么知乎如果明文保存这个密码,那么黑客就很容易窃取大家的密码来登陆,特别不安全。那么知乎就想到了一个方法,使用hash算法生成一个密码的签名,知乎后台只保存这个签名值。由于hash算法是不可逆的,那么黑客即便得到这个签名,也丝毫没有用处;而如果你在网站登陆界面上输入你的密码,那么知乎后台就会重新计算一下这个hash值,与网站中储存的原hash值进行比对,如果相同,证明你拥有这个账户的密码,那么就会允许你登陆。银行也是如此,银行是万万不敢保存用户密码的原文的,只会保存密码的hash值而而已。 在这些应用场景里,对于抗碰撞和抗篡改能力要求极高,对速度的要求在其次。一个设计良好的hash算法,其抗碰撞能力是很高的。以MD5为例,其输出长度为128位,设计预期碰撞概率为1/2^64,这是一个极小极小的数字——而即便是在MD5被王小云教授破解之后,其碰撞概率上限也高达1/2^41,也就是说,至少需要找2^40次才能有1/2的概率来找到一个与目标文件相同的hash值。而对于两个相似的字符串,MD5加密结果如下: ``` MD5("version1") = "966634ebf2fc135707d6753692bf4b1e"; MD5("version2") = "2e0e95285f08a07dea17e7ee111b21c8"; ``` 可以看到仅仅两个比特位(char("1")和char("2"))的改变,二者的MD5值就天差地别了。 到这里,读者估计会问,有没有可能找到这么一个算法,如果输出长度为128位,那么把这128位“充分利用到”,让它可以有种不同的hash值,而且分布均匀,抗篡改能力也特别高,一点点改动就会让hash值面目全非,一点都不浪费(这里的表述非常不严格)?稍微严格一点表述,就是:有没有这样一个算法,使得对于任何一个给定的输入,此算法都会输出一个固定的均匀随机的输出? 答案是密码学家们也至今没有构造出着这样一个算法,但是倾向于这个算法存在,而且有不少的密码学算法构造和这个假设有关。这个假设的名字叫做随机预言机(Random Oracle)。 在密码学中,hash算法有不少有意思的改进思路,以应付不同的使用场景。例如师兄 @刘巍然-学酥前一段时间让我写着玩的变色龙Hash(ChameleonHash),它有一个有趣的特性。在普通情况下,ChameleonHash可以当做普通hash算法使用,从明文(用m表示)得到的hash值(用h表示)抗碰撞能力依然特别强;但是如果使用者在计算这个hash值的时候预先计算一个值(用s表示)并保存,那么通过这个值很容易计算出另一个hash值也为h的明文m' !也就是说,如果你保留这个值的话,hash算法的抗碰撞能力完全被解除了。 这意味着,如果某个网站想要作恶的话,那么它可以很容易的替换他们自己的hash算法为ChameleonHash,方便地伪造出一个密钥来窃取用户的所有数据,而这个公司完全可以在对外宣传的时候,依然声称对用户信息严格保密——《教网站如何优雅地耍流氓》。 #回答二 转自:https://www.zhihu.com/question/26762707/answer/890181997 >提到hash,相信大多数同学都不会陌生,之前很火现在也依旧很火的技术区块链背后的底层原理之一就是hash,下面就从hash算法的原理和实际应用等几个角度,对hash算法进行一个讲解。 ##1、什么是Hash Hash也称散列、哈希,对应的英文都是Hash。基本原理就是把任意长度的输入,通过Hash算法变成固定长度的输出。这个映射的规则就是对应的Hash算法,而原始数据映射后的二进制串就是哈希值。活动开发中经常使用的MD5和SHA都是历史悠久的Hash算法。 ``` echo md5("这是一个测试文案"); // 输出结果:2124968af757ed51e71e6abeac04f98d ``` 在这个例子里,这是一个测试文案是原始值,2124968af757ed51e71e6abeac04f98d 就是经过hash算法得到的Hash值。整个Hash算法的过程就是把原始任意长度的值空间,映射成固定长度的值空间的过程。 ##2、Hash的特点 一个优秀的hash算法,需要什么样的要求呢? a)、从hash值不可以反向推导出原始的数据 这个从上面MD5的例子里可以明确看到,经过映射后的数据和原始数据没有对应关系 b)、输入数据的微小变化会得到完全不同的hash值,相同的数据会得到相同的值 ``` echo md5("这是一个测试文案"); // 输出结果:2124968af757ed51e71e6abeac04f98d echo md5("这是二个测试文案"); // 输出结果:bcc2a4bb4373076d494b2223aef9f702 ``` 可以看到我们只改了一个文字,但是整个得到的hash值产生了非常大的变化。 c)、哈希算法的执行效率要高效,长的文本也能快速地计算出哈希值 d)、hash算法的冲突概率要小 由于hash的原理是将输入空间的值映射成hash空间内,而hash值的空间远小于输入的空间。根据抽屉原理,一定会存在不同的输入被映射成相同输出的情况。那么作为一个好的hash算法,就需要这种冲突的概率尽可能小。 >桌上有十个苹果,要把这十个苹果放到九个抽屉里,无论怎样放,我们会发现至少会有一个抽屉里面放不少于两个苹果。这一现象就是我们所说的“抽屉原理”。抽屉原理的一般含义为:“如果每个抽屉代表一个集合,每一个苹果就可以代表一个元素,假如有n+1个元素放到n个集合中去,其中必定有一个集合里至少有两个元素。” 抽屉原理有时也被称为鸽巢原理。它是组合数学中一个重要的原理 ##3、Hash碰撞的解决方案 前面提到了hash算法是一定会有冲突的,那么如果我们如果遇到了hash冲突需要解决的时候应该怎么处理呢?比较常用的算法是链地址法和开放地址法。 ###3.1 链地址法 链表地址法是使用一个链表数组,来存储相应数据,当hash遇到冲突的时候依次添加到链表的后面进行处理。  链地址在处理的流程如下: 添加一个元素的时候,首先计算元素key的hash值,确定插入数组中的位置。如果当前位置下没有重复数据,则直接添加到当前位置。当遇到冲突的时候,添加到同一个hash值的元素后面,行成一个链表。这个链表的特点是同一个链表上的Hash值相同。java的数据结构HashMap使用的就是这种方法来处理冲突,JDK1.8中,针对链表上的数据超过8条的时候,使用了红黑树进行优化。由于篇幅原因,这里不深入讨论相关数据结构,有兴趣的同学可以参考这篇文章: 《Java集合之一—HashMap》 https://link.zhihu.com/?target=https%3A//blog.csdn.net/woshimaxiao1/article/details/83661464 ###3.2 开放地址法 开放地址法是指大小为 M 的数组保存 N 个键值对,其中 M > N。我们需要依靠数组中的空位解决碰撞冲突。基于这种策略的所有方法被统称为“开放地址”哈希表。线性探测法,就是比较常用的一种“开放地址”哈希表的一种实现方式。线性探测法的核心思想是当冲突发生时,顺序查看表中下一单元,直到找出一个空单元或查遍全表。简单来说就是:一旦发生冲突,就去寻找下 一个空的散列表地址,只要散列表足够大,空的散列地址总能找到。 线性探测法的数学描述是:h(k, i) = (h(k, 0) + i) mod m,i表示当前进行的是第几轮探查。i=1时,即是探查h(k, 0)的下一个;i=2,即是再下一个。这个方法是简单地向下探查。mod m表示:到达了表的底下之后,回到顶端从头开始。 对于开放寻址冲突解决方法,除了线性探测方法之外,还有另外两种比较经典的探测方法,二次探测(Quadratic probing)和双重散列(Double hashing)。但是不管采用哪种探测方法,当散列表中空闲位置不多的时候,散列冲突的概率就会大大提高。为了尽可能保证散列表的操作效率,一般情况下,我们会尽可能保证散列表中有一定比例的空闲槽位。我们用装载因子(load factor)来表示空位的多少。 散列表的装载因子=填入表中的元素个数/散列表的长度。装载因子越大,说明冲突越多,性能越差。 ###3.3 两种方案的demo示例 假设散列长为8,散列函数H(K)=K mod 7,给定的关键字序列为{32,14,23,2, 20}当使用链表法时,相应的数据结构如下图所示: 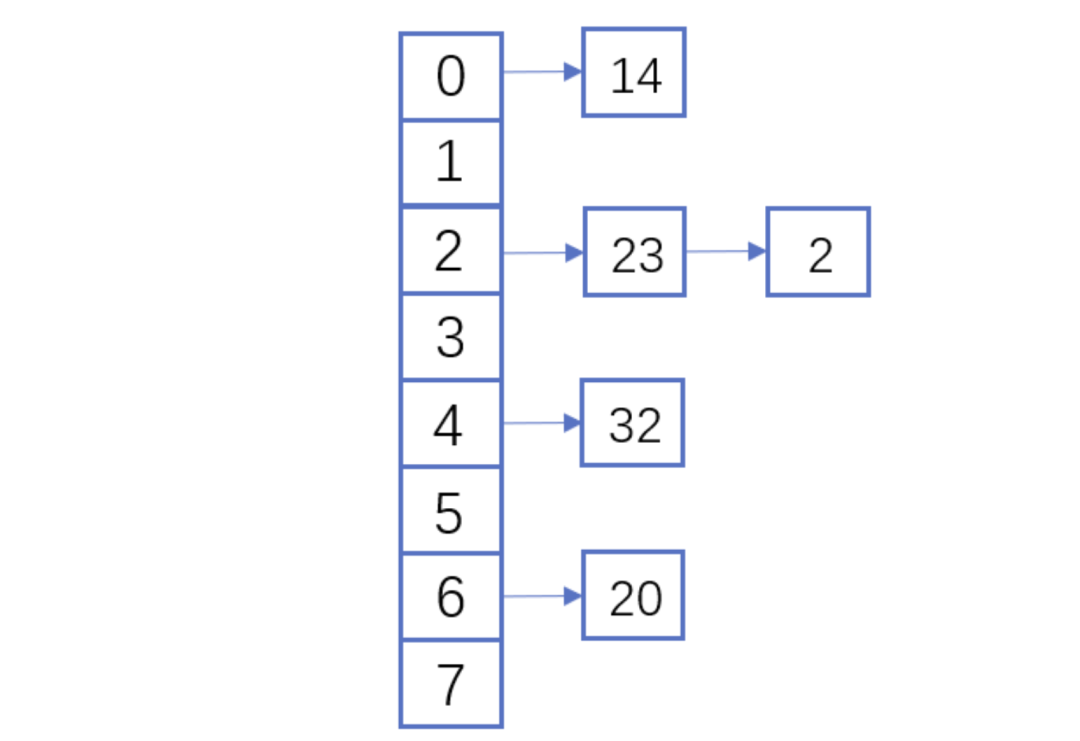 当使用线性探测法时,相应的数据结果如下图所示: 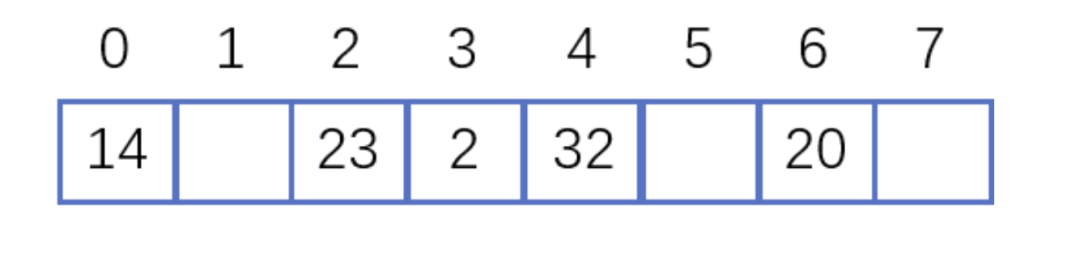 这里的两种算法的区别是2这个元素,在链表法中还是在节点2的位置上,但是在线性探测法遇到冲突时会将冲突数据放到下一个空的位置下面。 ##4、hash算法在日常活动中的应用 在日常运营活动中,我们活动开发经常遇到的应用场景是信息加密、数据校验、负载均衡。下面分别对这三种应用场景进行讲解。 ###4.1 信息加密 首先我们看一下信息加密的应用。2011年CSDN脱库事件,导致超过600W的用户的密码泄露,让人失望的是,CSDN是明文存储用户的注册邮箱和密码的。作为用户的非常隐私的信息,最简单的保护措施就是对密码进行hash加密。在客户端对用户输入的密码进行hash运算,然后在服务端的数据库中保存用户密码的hash值。由于服务器端也没有存储密码的明文,所以目前很多网站也就不再有找回密码的功能了。 这里也友情提示一下大家:如果在使用中发现某网站还有提供找回密码的功能,就要好好担心下这个网站的安全性了。 看到这里有些同学会觉得那么我们是不是对用户输入的密码进行一次MD5加密就可以了呢,这样就算恶意用户知道了hash值,也没有办法拿到用户的真实密码。假设用户的密码是123456789,经过一次md5以后得到的值是:25f9e794323b453885f5181f1b624d0b 那么是不是使用了这个加密后的字符串来存密码就万无一失了呢,理想总是很丰满,而现实总是很骨感的。大家可以看一下这个网站: https://www.cmd5.com/ 这里是该网站的相关介绍: >本站针对md5、sha1等全球通用公开的加密算法进行反向查询,通过穷举字符组合的方式,创建了明文密文对应查询数据库,创建的记录约90万亿条,占用硬盘超过500TB,查询成功率95%以上,很多复杂密文只有本站才可查询。已稳定运行十余年,国内外享有盛誉 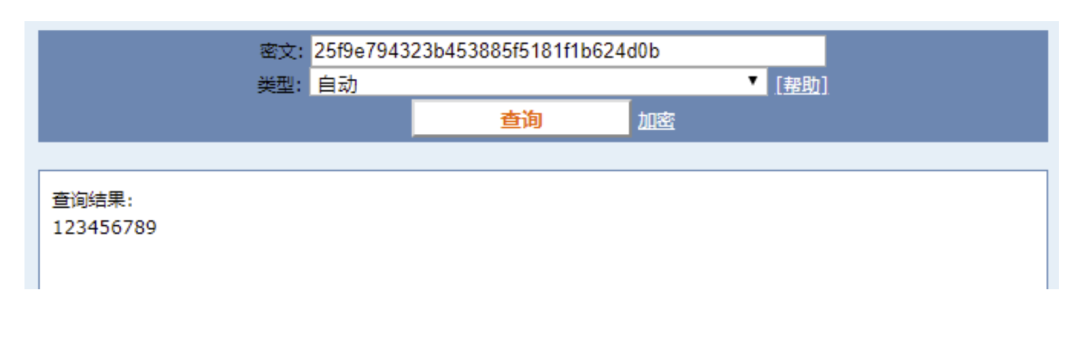 那么一般针对这种问题,我们的解决之道就是引入salt(加盐),即利用特殊字符(盐)和用户的输入合在一起组成新的字符串进行加密。通过这样的方式,增加了反向查询的复杂度。但是这样的方式也不是万无一失,如果发生了盐被泄露的问题,就需要所有用到的地方来重置密码。 针对salt泄露的问题,其实还有一种解决办法,即使用HMAC进行加密(Hash-based Message Authentication Code)。这种算法的核心思路是加密使用的key是从服务器端获取的,每一个用户的是不一样的。如果发生了泄露,那么也就是这一个用户的会被泄露,不会影响到全局。 这里也留给大家一个思考点,如果恶意用户直接抓取了你的活动参与链接,也就是拿到了你计算后的hash值,那从技术的角度上说,我们还有没有其他可以提升恶意用户的违法成本呢? ###4.2 数据校验 - git commit id 使用过git的同学都应该清楚,每次git提交后都有一个commit id,比如:19d02d2cc358e59b3d04f82677dbf3808ae4fc40 就是一次git commit的结果,那么这个id是如何生成出来的呢?查阅了相关资料,使用如下代码可以进行查看: ``` printf "commit %s\0" $(git cat-file commit HEAD | wc -c); git cat-file commit HEAD ``` git的commit id主要包括了以下几部分内容:Tree 哈希,parent哈希、作者信息和本次提交的备注。 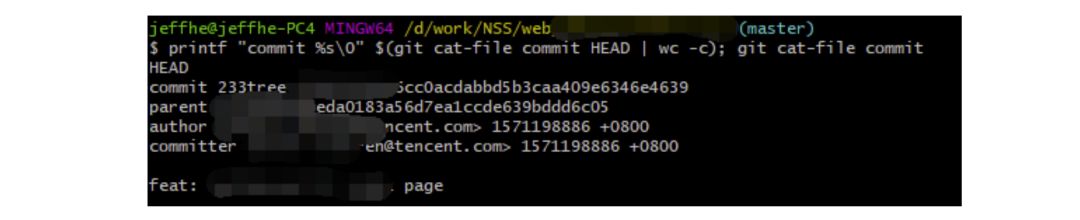 >针对这些信息进行SHA-1 算法后得到值就是本次提交的commit id。简单来讲,就是对于单次提交的头信息的一个校验和。 Linux kernel开创者和Git的开发者——Linus说,Git使用了sha1并非是为了安全性,而是为了数据的完整性;它可以保证,在很多年后,你重新checkout某个commit时,一定是它多年前的当时的状态,完全一摸一样,完全值得信任。 但最新研究表明,理论上对其进行哈希碰撞(hash collision,不同的两块数据有相同的hash值)的攻击可以在2^51(2的51次方)左右的次数内实现。不过由于commit id 是针对单个仓库里的,所以实际应用中我们可以认为如果两个文件的SHA-1值是相同的,那么它们确是完全相同的内容。 *注:对于git里tree、parent等结构感兴趣的同学,可以参考下这篇文章《Git 内部原理 - Git 对象》,这里由于篇幅原因就不进行深入分析了。 - 版权校验 在数据校验方面的另一个应用场景就是版权的保护或者违禁信息的打击,比如某个小视频,第一个用户上传的时候,我们认为是版权所有者,计算一个hash值存下来。当第二个用户上传的时候,同样计算hash值,如果hash值一样的话,就算同一个文件。这种方案其实也给用户传播违禁文件提高了一些门槛,不是简单的换一个名字或者改一下后缀名就可以躲避掉打击了。(当然这种方式也是可以绕过的,图片的你随便改一下颜色,视频去掉一帧就又是完全不同的hash值了。注意:我没有教你变坏,我只是和你在讨论这个技术。。。)另外我们在社区里,也会遇到玩家重复上传同一张图片或者视频的情况,使用这种校验的方式,可以有效减少cos服务的存储空间。 - 大文件分块校验 使用过bt的同学都有经验,在p2p网络中会把一个大文件拆分成很多小的数据各自传输。这样的好处是如果某个小的数据块在传输过程中损坏了,只要重新下载这个块就好。为了确保每一个小的数据块都是发布者自己传输的,我们可以对每一个小的数据块都进行一个hash的计算,维护一个hash List,在收到所有数据以后,我们对于这个hash List里的每一块进行遍历比对。这里有一个优化点是如果文件分块特别多的时候,如果遍历对比就会效率比较低。可以把所有分块的hash值组合成一个大的字符串,对于这个字符串再做一次Hash运算,得到最终的hash(Root hash)。在实际的校验中,我们只需要拿到了正确的Root hash,即可校验Hash List,也就可以校验每一个数据块了。 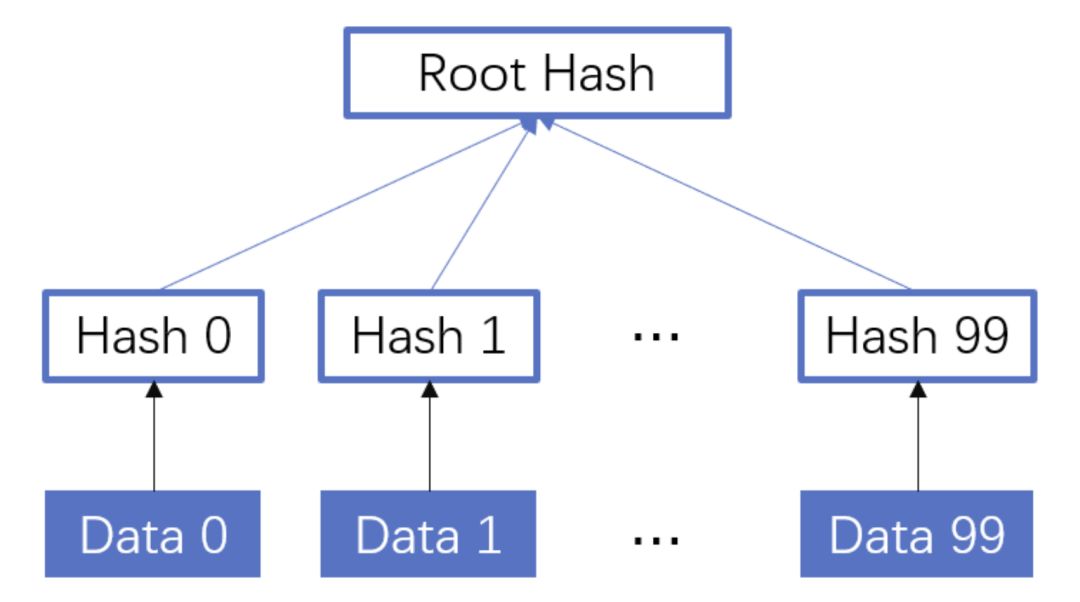 ###4.3 负载均衡 活动开发同学在应对高星级业务大用户量参与时,都会使用分库分表,针对用户的openid进行hashtime33取模,就可以得到对应的用户分库分表的节点了。 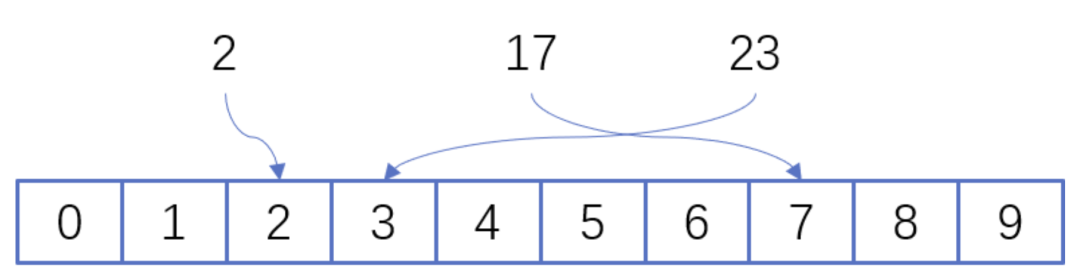 如上图所示,这里其实是分了10张表,openid计算后的hash值取模10,得到对应的分表,在进行后续处理就好。对于一般的活动或者系统,我们一般设置10张表或者100张表就好。 下面我们来看一点复杂的问题,假设我们活动初始分表了10张,运营一段时间以后发现需要10张不够,需要改到100张。这个时候我们如果直接扩容的话,那么所有的数据都需要重新计算Hash值,大量的数据都需要进行迁移。如果更新的是缓存的逻辑,则会导致大量缓存失效,发生雪崩效应,导致数据库异常。造成这种问题的原因是hash算法本身的缘故,只要是取模算法进行处理,则无法避免这种情况。针对这种问题,我们就需要利用一致性hash进行相应的处理了。 一致性hash的基本原理是将输入的值hash后,对结果的hash值进行2^32取模,这里和普通的hash取模算法不一样的点是在一致性hash算法里将取模的结果映射到一个环上。将缓存服务器与被缓存对象都映射到hash环上以后,从被缓存对象的位置出发,沿顺时针方向遇到的第一个服务器,就是当前对象将要缓存于的服务器,由于被缓存对象与服务器hash后的值是固定的,所以,在服务器不变的情况下,一个openid必定会被缓存到固定的服务器上,那么,当下次想要访问这个用户的数据时,只要再次使用相同的算法进行计算,即可算出这个用户的数据被缓存在哪个服务器上,直接去对应的服务器查找对应的数据即可。这里的逻辑其实和直接取模的是一样的。如下图所示: 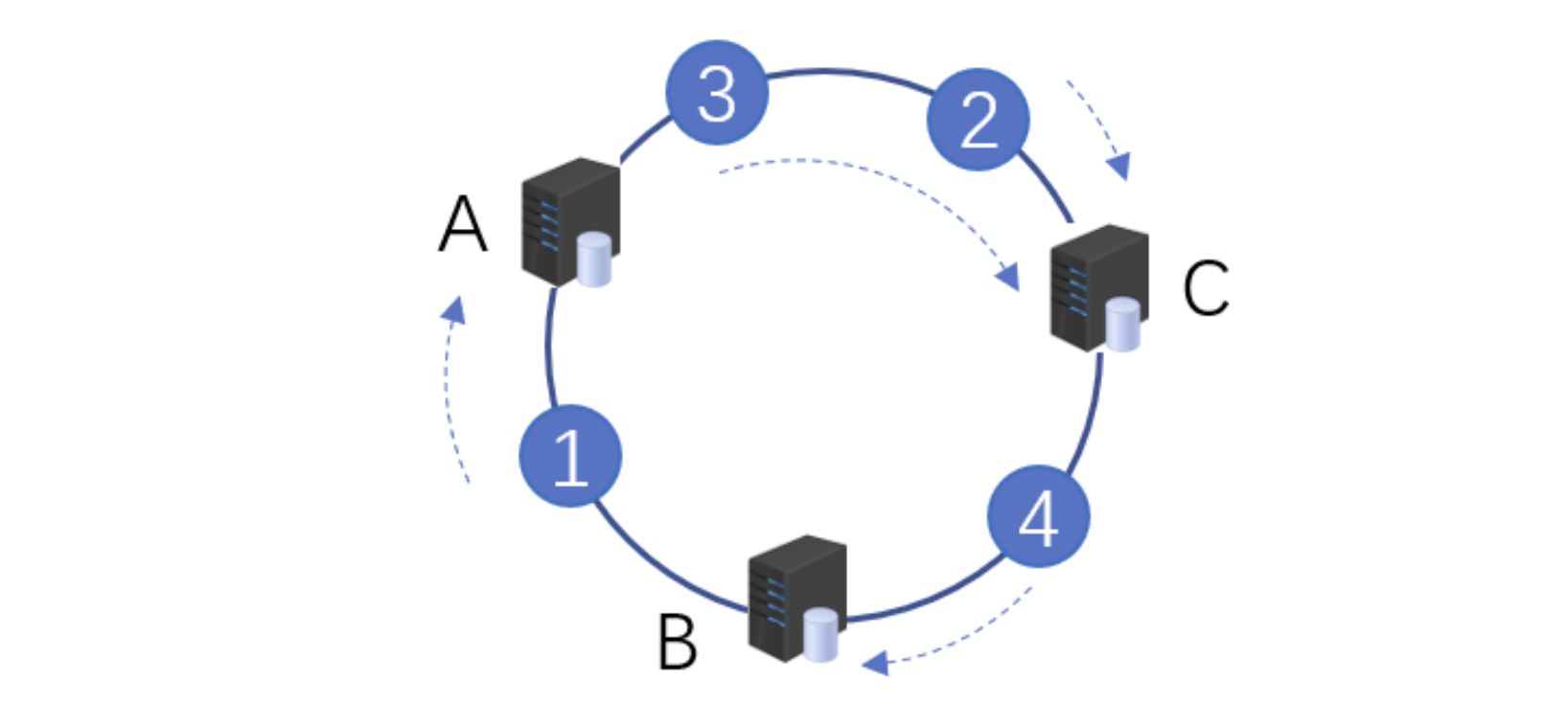 初始情况如下:用户1的数据在服务器A里,用户2、3的数据存在服务器C里,用户4的数据存储在服务器B里 下面我们来看一下当服务器数量发生变化的时候,相应影响的数据情况: - 服务器缩容 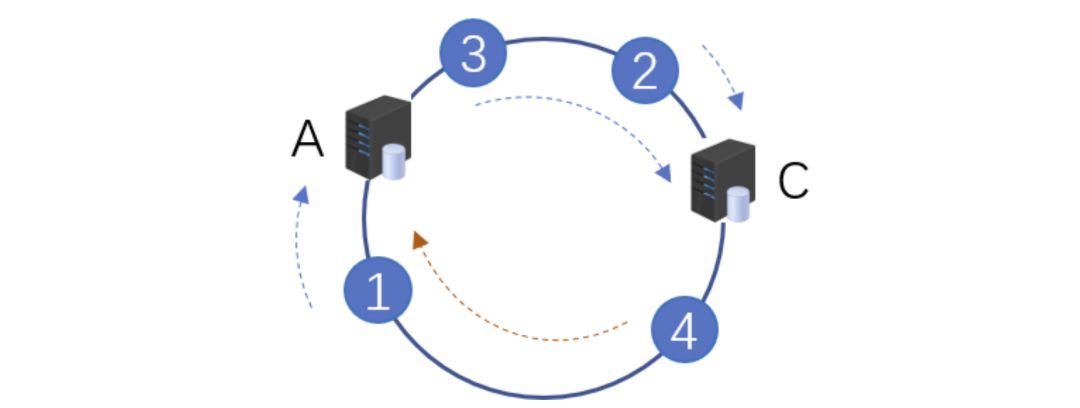 服务器B发生了故障,进行剔除后,只有用户4的数据发生了异常。这个时候我们需要继续按照顺时针的方案,把缓存的数据放在用户A上面。 - 服务器扩容 同样的,我们进行了服务器扩容以后,新增了一台服务器D,位置落在用户2和3之间。按照顺时针原则,用户2依然访问的是服务器C的数据,而用户3顺时针查询后,发现最近的服务器是D,后续数据就会存储到d上面。 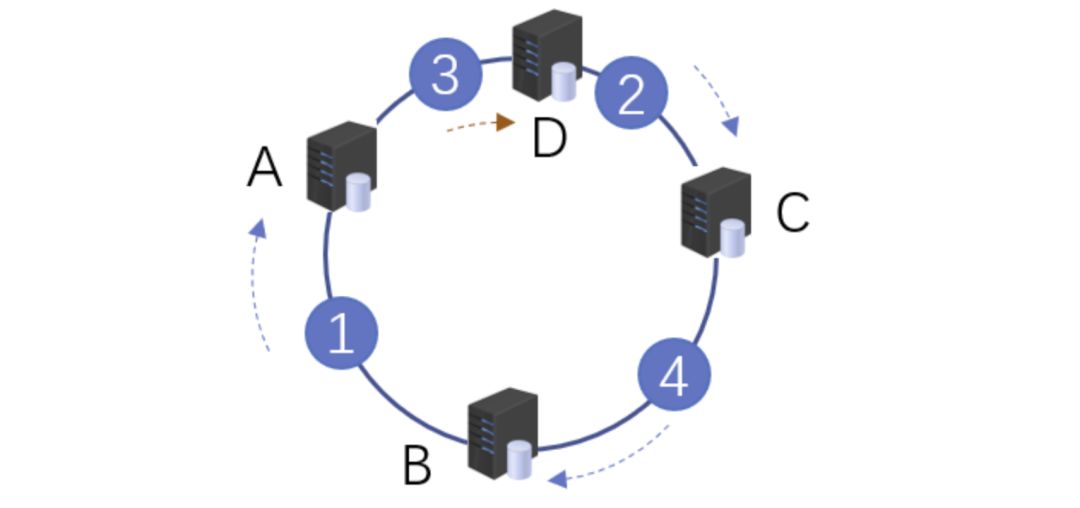 - 虚拟节点 当然这只是一种理想情况,实际使用中,由于服务器节点数量有限,有可能出现分布不均匀的情况。这个时候会出现大量数据都被映射到某一台服务器的情况,如下图左侧所示。为了解决这个问题,我们采用了虚拟节点的方案。虚拟节点是实际节点(实际的物理服务器)在hash环上的复制品,一个实际节点可以对应多个虚拟节点。虚拟节点越多,hash环上的节点就越多,数据被均匀分布的概率就越大。 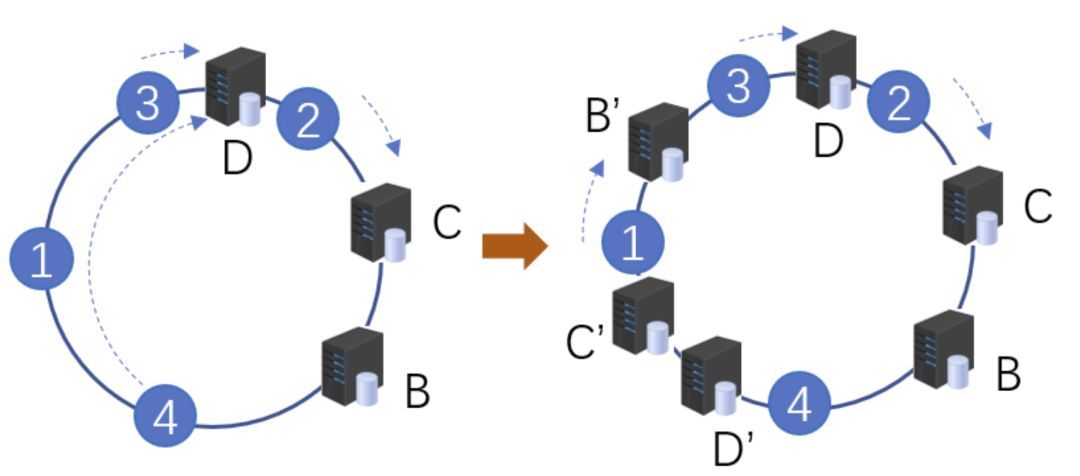 如右图所示,B、C、D 是原始节点复制出来的虚拟节点,原本都要访问机器D的用户1、4,分别被映射到了B,D。通过这样的方式,起到了一个服务器均匀分布的作用。 ##5、几种hash算法的扩展应用 下面介绍几种大家可能不经常遇到的应用,由于篇幅原因,不做深入介绍,只抛砖引玉。 ###5.1 SimHash simHash是google用于海量文本去重的一种方法,它是一种局部敏感hash。那什么叫局部敏感呢,假定两个字符串具有一定的相似性,在hash之后,仍然能保持这种相似性,就称之为局部敏感hash。普通的hash是不具有这种属性的。simhash被Google用来在海量文本中去重。 simHash算法的思路大致如下: - 将Doc进行关键词抽取(其中包括分词和计算权重),抽取出n个(关键词,权重)对, 即图中的多个(feature, weight)。记为 feature_weight_pairs = [fw1, fw2 … fwn],其中 fwn = (feature_n,weight_n)。 - 对每个feature_weight_pairs中的feature进行hash。然后对hash_weight_pairs进行位的纵向累加,如果该位是1,则+weight,如果是0,则-weight,最后生成bits_count个数字,大于0标记1,小于0标记0 - 最后转换成一个64位的字节,判断重复只需要判断他们的特征字的距离是不是 < n(n根据经验一般取3),就可以判断两个文档是否相似。  如下图所示,当两个文本只有一个字变化时,如果使用普通Hash则会导致两次的结果发生较大改变,而SimHash的局部敏感特性,会导致只有部分数据发生变化。 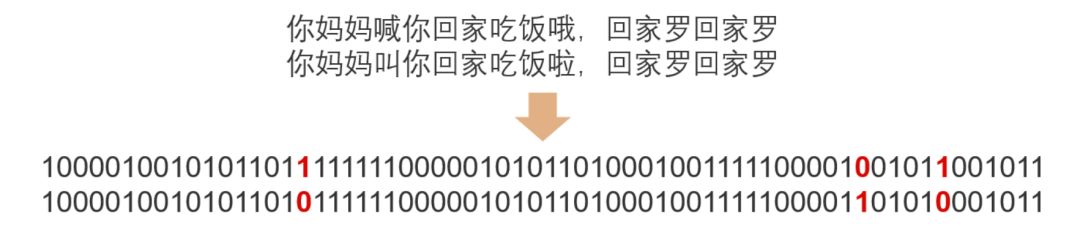 ###5.2 GeoHash GeoHash将地球作为为一个二维平面进行递归分解。每个分解后的子块在一定经纬度范围内拥有相同的编码。以下图为例,这个矩形区域内所有的点(经纬度坐标)都共享相同的GeoHash字符串,这样既可以保护隐私(只表示大概区域位置而不是具体的点),又比较容易做缓存。 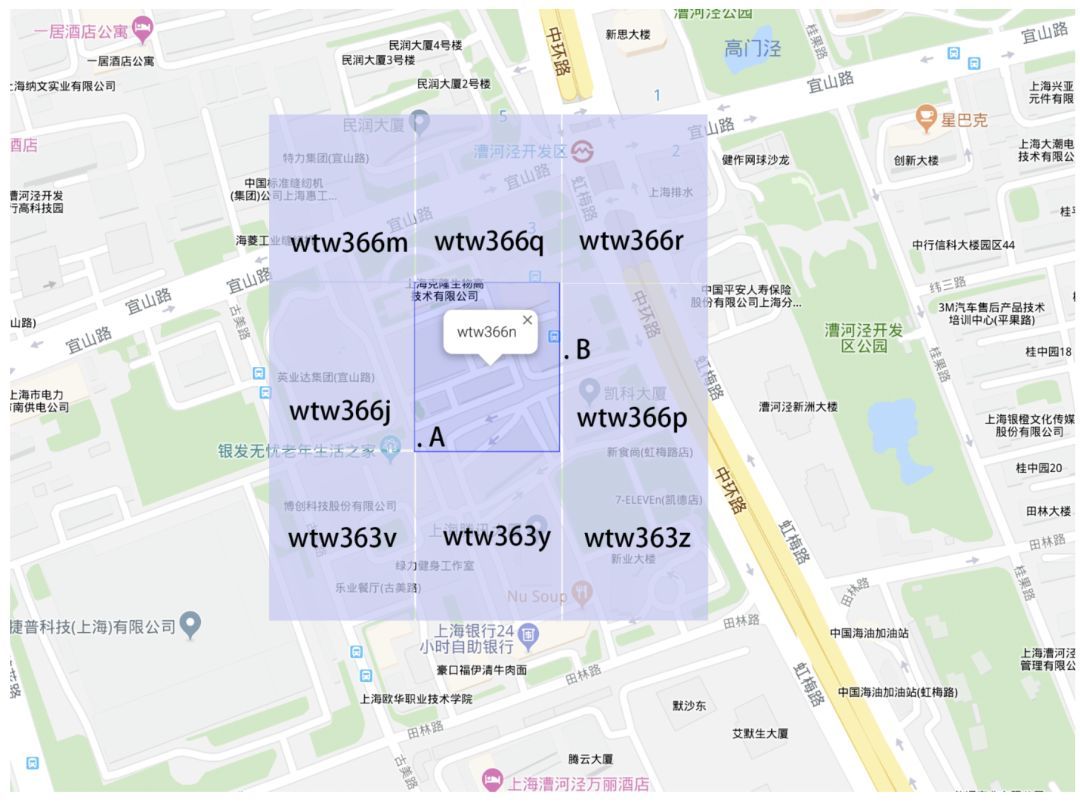 下面以一个例子来理解下这个算法,我们对纬度39.3817进行逼近编码 : - 地球纬度区间是[-90,90],对于这个区间进行二分划分左区间[-90,0), 右区间[0,90]。39.3817属于右区间,标记为1 - 将右区间[0,90]继续进行划分,左区间[0,45) ,右区间[45,90]。39.3817属于左区间,标记为0 - 递归上面的过程,随着每次迭代,区间[a,b]会不断接近39.3817。递归的次数决定了生成的序列长度。 - 对于经度做同样的处理。得到的字符串,偶数位放经度,奇数位放纬度,把2串编码组合生成新串。对于新串转成对应10进制查出实际的base32编码就是类似WX4ER的hash值。 整体递归过程如下表所示: 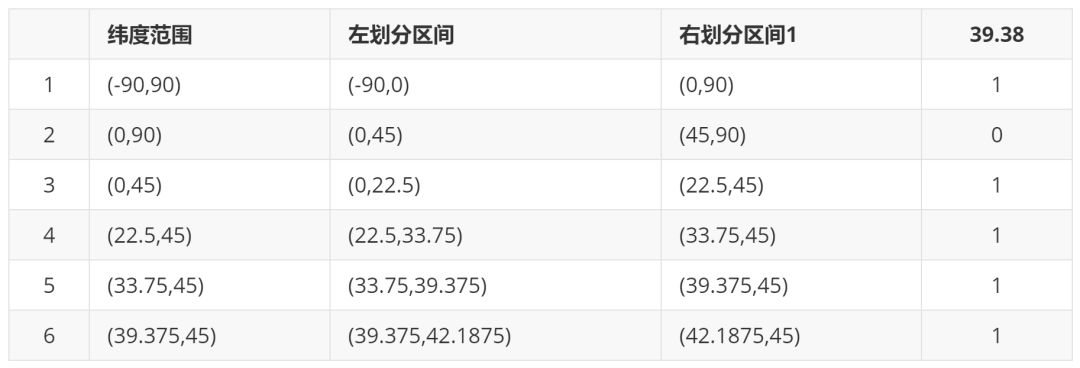 这里有一篇文章详细介绍了GeoHash,有兴趣的同学可以移步这里: 腾讯技术工程:app 是如何快速定位我们位置的?深入了解 geohash 算法及其实现 https://zhuanlan.zhihu.com/p/90889887 ###5.3 布隆过滤器 布隆过滤器被广泛用于黑名单过滤、垃圾邮件过滤、爬虫判重系统以及缓存穿透问题。对于数量小,内存足够大的情况,我们可以直接用hashMap或者hashSet就可以满足这个活动需求了。但是如果数据量非常大,比如5TB的硬盘上放满了用户的参与数据,需要一个算法对这些数据进行去重,取得活动的去重参与用户数。这种时候,布隆过滤器就是一种比较好的解决方案了。 布隆过滤器其实是基于bitmap的一种应用,在1970年由布隆提出的。它实际上是一个很长的二进制向量和一系列随机映射函数,用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都远远超过一般的算法,缺点是有一定的误识别率和删除困难,主要用于大数据去重、垃圾邮件过滤和爬虫url记录中。核心思路是使用一个bit来存储多个元素,通过这样的方式来减少内存的消耗。通过多个hash函数,将每个数据都算出多个值,存放在bitmap中对应的位置上。 布隆过滤器的原理见下图所示: 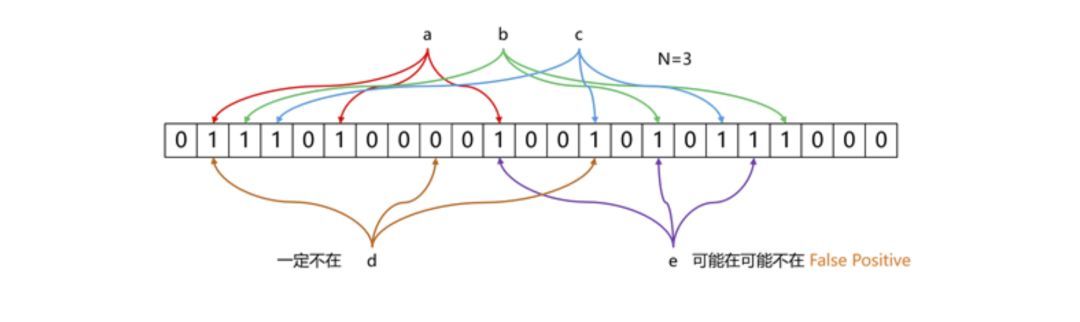 上图所示的例子中,数据a、b、c经过三次hash映射后,对应的bit位都是1,表示这三个数据已经存在了。而d这份数据经过映射后有一个结果是0,则表明d这个数据一定没有出现过。布隆过滤器存在假阳率(判定存在的元素可能不存在)的问题,但是没有假阴率(判断不存在的原因可能存在)的问题。即对于数据e,三次映射的结果都是1,但是这份数据也可能没有出现过。 误判率的数据公式如下所示: 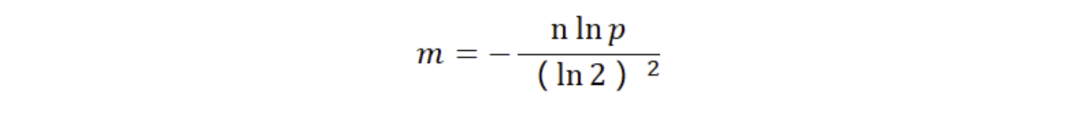 其中,p是误判率,n是容纳的元素,m是需要的存储空间。由公示可以看出,布隆过滤器的长度会直接影响误报率,布隆过滤器越长其误报率越小。哈希函数的个数也需要权衡,个数越多则布隆过滤器 bit 位置位 1 的速度越快,且布隆过滤器的效率越低;但是如果太少的话,则会导致误报率升高。 ##6、总结 Hash算法作为一种活动开发经常遇到的算法,我们在使用中不仅仅要知道这种算法背后真正的原理,才可以在使用上做到有的放矢。Hash的相关知识还有很多,有兴趣的同学可以继续深入研究。 更多内容欢迎关注我们:腾讯技术工程https://zhuanlan.zhihu.com/tencent-TEG #回答三 转自:https://www.zhihu.com/question/26762707/answer/418939144 ##1. 相关介绍 在哈希表中,记录的存储位置 = f (关键字),通过查找关键字的存储位置即可,不用进行比较。散列技术是在记录的存储位置和它的关键字之间建立一个明确的对应关系f 函数,使得每个关键字 key 对应一个存储位置 f(key) 且这个位置是唯一的。这里我们将这种对应关系 f 称为散列函数,又称为哈希(Hash)函数。采用散列技术将记录存储在一块连续的存储空间中,这块连续存储空间称为散列表或哈希表(Hash table)。 当存储记录时,通过散列函数计算出记录的散列地址;当查找记录时,我们通过同样的是散列函数计算记录的散列地址,并按此散列地址访问该记录。散列技术即使一种存储方法,也是一种查找方法;散列技术之间没有关系,只有关键字和函数之间有关系,所以散列技术是一种面向查找的存储技术 缺点是会存在关键字重复的问题,比如说男女为关键字的时候就不合适了。同样不适合查找范围的,比如说查找18-20岁之间的同学。散列表技术对于1对1的查找是适合的。 ##2. 构造散列函数 ###2.1 两个基本原则 “好的散列函数 = 计算简单 + 分布均匀”。其中计算简单指的是散列函数的计算时间不应该超过其他查找技术与关键字比较的时间,而分布均匀指的是散列地址分布均匀。 ###2.2 具体方法 ####2.2.1 直接定址法 即使用关键字本身作为函数值,即f(key) = key。假如有一个从1到100岁的人口数字统计表,其中,年龄作为关键字,哈希函数取关键字自身。 如,下图所示 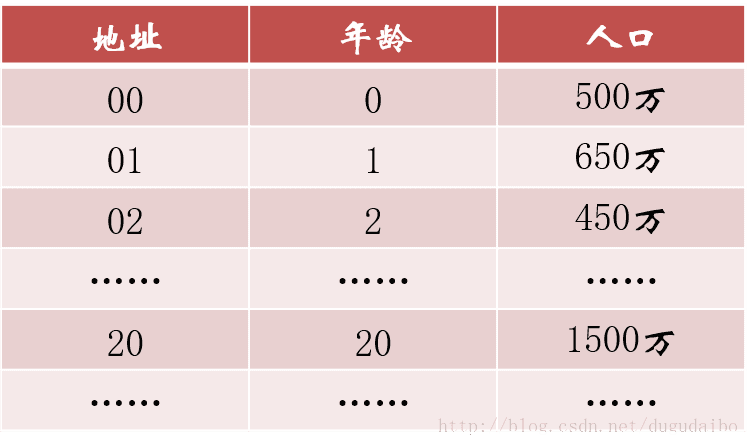 又假果现在要统计的是1980年以后出生的人口数,那么我们对出生年份这个关键字可以变换为:用年份减去1980的值来作为地址。即:f(key) = key – 1980  所以直接定值法是取关键字的某个线性函数值为散列地址,即 `f(key) = a*key + b`。其优点是简单、均匀,不会产生冲突;但缺点是需要知道关键字的分布情况,希望数值是连续的。 ####2.2.2 数字分析法 数字分析法通常适合处理关键字位数比较大的情况,例如我们现在要存储某家公司员工登记表,如果用手机号作为关键字,那么我们发现抽取后面的四位数字作为散列地址是不错的选择,如下图所示  ####2.2.3 平方取中法 平方取中法是将关键字平方之后取中间若干位数字作为散列地址。这种方法适用于不知道关键字的分布,且数值的位数又不是很大的情况。 ####2.2.4 折叠法 折叠法是将关键字从左到右分割成位数相等的几部分,然后将这几部分叠加求和,并按散列表表长取后几位作为散列地址。 ####2.2.5 除留余数法 此方法为最常用的构造散列函数方法,对于散列表长为m的散列函数计算公式为: f(key) = key mod p(p<=m) 事实上,这个方法不仅可以对关键字直接取模,也可以通过折叠、平方取中后再取模。例如下表,我们对有12个记录的关键字构造散列表时,就可以用f(key) = key mod 12的方法。  p的选择是关键,如果对于这个表格的关键字,p还选择12的话,那得到的情况未免也太糟糕了:  p的选择很重要,如果我们把p改为11,那结果就另当别论啦:  当然在上述的这种情况中仍然是有冲突的情况,对于这种情况在后面中会介绍解决的方法。 ####2.2.6 随机数法 选择一个随机数,取关键字的随机函数值为它的散列地址。 f(key) = random(key)。 这里的random是随机函数,当关键字的长度不等时,采用这个方法构造散列函数是比较合适的。 ###2.3 哈希表的选择 现实中,我们应该视不同的情况采用不同的散列函数,这里给大家一些参考方向: (1) 计算散列地址所需的时间; (2) 关键字的长度; (3) 列表的大小; (4) 关键字的分布情况; (5) 记录查找的频率。 ##3. 处理散列冲突的方法 ###3.1 开放定址法 所谓的开放定址法就是一旦发生了冲突,就去寻找下一个空的散列地址,只要散列表足够大,空的散列地址总能找到,并将记录存入。它的公式是: fi(key) = (f(key)+di) MOD m (di=1,2,…,m-1) 例:假设关键字集合为{12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 34},使用除留余数法(m=12)求散列表  也可以修改di的取值方式,例如使用平方运算来尽量解决堆积问题: fi(key) = (f(key)+di) MOD m (di=1²,-1²,2²,-2²…,q²,-q²,q<=m/1) 还有一种方法是,在冲突时,对于位移量di采用随机函数计算得到,我们称之为随机探测法: fi(key) = (f(key)+di) MOD m (di是由一个随机函数获得的数列) ###3.2 再散列函数法 同时准备多个散列函数,当第一个散列函数发生冲突的时候可以用备选的散列函数进行计算。 ###3.3 链地址法 例:假设关键字集合为{12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 34},同样使用除留余数法求散列表,如下图所示  在上面个的链表中,如果没有发生冲突的话,元素后面的地址为空;如果有冲突的话就将他链接到下一个元素。 ###3.4 公共溢出区法 例:假设关键字集合为{12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 34},同样使用除留余数法求散列表,如下图所示  没有冲突的元素放在左边的表,有冲突的元素,将多余的元素放在右边的那个表。 ##4. 散列表查找的代码实现 在这里采用除留余数法构造散列函数,代码中还包括散列表的结构定义,散列表的初始化,插入关键字和查找关键字 ``` #define HASHSIZE 12 #define NULLKEY -32768 // 定义一个散列表的结构 typedef struct { int *elem; // 数据元素的基址,动态分配数组 int count; // 当前数据元素的个数 }HashTable; // 初始化散列表 int InitHashTable(HashTable *H) { H->count = HASHSIZE; H->elem = (int *)malloc(HASHSIZE * sizeof(int)); if( !H->elem ) { return -1; //申请空间失败 } for( i=0; i < HASHSIZE; i++ ) { H->elem[i] = NULLKEY; //迭代进行初始化,其中的NULLKEY是一个默认值 } return 0; } // 使用除留余数法 int Hash(int key) { return key % HASHSIZE; //除数一般小于等于表长 } // 插入关键字到散列表 void InsertHash(HashTable *H, int key) { int addr; addr = Hash(key); //只是得到一个偏移地址 while( H->elem[addr] != NULLKEY ) // 如果不为空,则冲突出现 { addr = (addr + 1) % HASHSIZE; // 开放定址法的线性探测 } H->elem[addr] = key; } // 散列表查找关键字 int SearchHash(HashTable H, int key, int *addr) { *addr = Hash(key); while( H.elem[*addr] != key ) { *addr = (*addr + 1) % HASHSIZE; if( H.elem[*addr] == NULLKEY || *addr == Hash(key) ) //后面那个条件说明循环回到原点 { return -1; } } return 0; } ``` 标签: hash 本作品采用 知识共享署名-相同方式共享 4.0 国际许可协议 进行许可。